Vertical angles are congruent.
From the figure, angle 3 and angle (7x + 3) are vertical angles, therefore angle 3 is (7x + 3)
Angle 1 and 127 degrees are supplementary angles and have a sum of 180 degrees.
That will be :
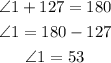
Angle 2 and 133 degrees are also supplementary angles and have a sum of 180 degrees.
That will be :
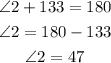
Now we have angles 1, 2 and 3 which are angles in a triangle, and the sum of interior angles in a triangle is 180 degrees.
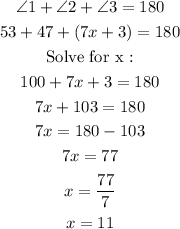
ANSWER :
x = 11