This problem is an application of the Geometric mean theorem. It says that
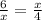
Comment: In other words, it says that the length of BC (x) is the geometric mean between the lengths of AC and DC.
Then,
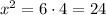
![x=\sqrt[]{24}=2\cdot\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/udf2l2b5feesu5j70qbg2k9u3uerilmlql.png)
................................................................................................................................................................
Let's talk a little about the simplest radical form of a square root
![\sqrt[]{a}](https://img.qammunity.org/2023/formulas/mathematics/college/m1ip7g781luw7lccygc5ixob3v4mzsmcaw.png)
The first step to finding it is to write the number within the root as a product of prime powers, such product is called its integer factorization. Let's do that for 24:
Then, the integer factorization of 24 is

Thus,
![\sqrt[]{24}=\sqrt[]{2^3\cdot3}](https://img.qammunity.org/2023/formulas/mathematics/college/y2d4oovpy9z4f4mlatkbkdbrbh5ytbulvu.png)
The idea now is to take out of the root all we can. The rule is that we can only take out powers of 2 (for our root is a square root). In the expression
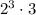
There is only one power of 2, within 2^3. We can write it as
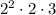
How are we going to take out it? We are going to take out the base of the power, which is 2 in this case. Then,
![\sqrt[]{24}=2\cdot\sqrt[]{2\cdot3}=2\cdot\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/xbvvha0ivasojuxb810zhnrtri5u0dlemj.png)
In simple terms, the simplest radical form of a root is what results after taking out the root all that can be taken out.