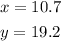Question

Can you please solve the last question… number 3! Thanks!

Answer 1

Let us break the shape into two triangles and solve for the unknowns.

The first triangle is shown below:

We will use the Pythagorean Theorem defined to be:

`\begin{gathered} c^2=a^2+b^2 \\ where\text{ c is the hypotenuse and a and b are the other two sides} \end{gathered}`

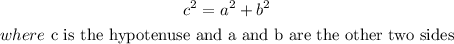
Therefore, we can relate the sides of the triangles as shown below:

`25^2=y^2+16^2`

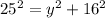
Solving, we have:

`\begin{gathered} y^2=25^2-16^2 \\ y^2=625-256 \\ y^2=369 \\ y=√(369) \\ y=19.2 \end{gathered}`

Hence, we can have the second triangle to be:

Applying the Pythagorean Theorem, we have:

`22^2=x^2+19.2^2`

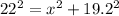
Solving, we have:

`\begin{gathered} 484=x^2+369 \\ x^2=484-369 \\ x^2=115 \\ x=√(115) \\ x=10.7 \end{gathered}`

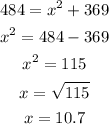
The values of the unknowns are:

`\begin{gathered} x=10.7 \\ y=19.2 \end{gathered}`