From the given picture we can see
ACB is a right triangle at C
AC = b
CB = a
AB = c
Since mSince a = 5 ft
Then to find b and c we will use the trigonometry ratios

Substitute the value of sin 60
![\begin{gathered} \sin 60=\frac{\sqrt[]{3}}{2} \\ \frac{\sqrt[]{3}}{2}=(5)/(c) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wnhm6uwa0c70zst9j8uxlgk4ngisqsaxmt.png)
By using the cross multiplication
![\begin{gathered} \sqrt[]{3}* c=2*5 \\ \sqrt[]{3}c=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k460q6to7o4p1o0sj2hp8cy6inl52nib2q.png)
Divide both sides by root 3
![\begin{gathered} \frac{\sqrt[]{3}c}{\sqrt[]{3}}=\frac{10}{\sqrt[]{3}} \\ c=\frac{10}{\sqrt[]{3}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/73utexs1i2c5uos5emkn5b58a3w6merpvs.png)
To find b we will use the tan ratio
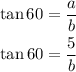
Substitute the value of tan 60
![\begin{gathered} \tan 60=\sqrt[]{3} \\ \sqrt[]{3}=(5)/(b) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i4qpj0lnu6hfk90h7eyuatmk3mh31nbhvp.png)
Switch b and root 3
![b=\frac{5}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/7pwtsshn9wy0u7i8cmpaifscbaiktbsmmu.png)
The exact values of b and c are
![\begin{gathered} b=\frac{5}{\sqrt[]{3}} \\ c=\frac{10}{\sqrt[]{3}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/69n5ga6xljq7iapgeokvgw1llwj33ffviz.png)