A direct proportional relation can always be express as an equation of the form:
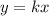
where k is the constant of proportionality. (This means that y has to be the result of multiplying a number by x)
Now, let's see at the option we have.
a)
Solving the equation for y we have:
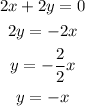
Since we can write the equation in the form as a direct proportional relationship we conclude that option a shows a directly proportional relationship and that the constant is -1.
b)
For this case we have the equation:
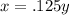
From it we already can see that this means that x is directly proportional to y and that the constatn of porportionality is 0.125.
Now if we want we can solve the equation for y, then we have:
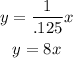
this equation shows that y is directly proportional to x and that the constant of proportionality is 8.
Notice that the the constant of proportionality changes if we write the relation as x directly proportional to y or if we write it as y directly proportional to x. Either way the relation express the same and it is directly proportional.
c) and d)
For this equations that we have a division in which one of the variables is the divisor (or the denominator); this means that the equation show a relation between x and y but their are not directly proportional. In fact this means that the equations show an inversely proportional relations.