Question

Jerry, Jack and Sophie are all hoping to save money! Jerry thinks saving money in a shoe box in his closet every month is a good idea. He decides to start with $125, and then save $50 each month. Jack was given $3520 from his Grandma, and decides to put the money into an account that has a 6.5% interest rate that is compounded annually. Sophie has earned $3500 working at the movie theater decides to put her money in the bank in an account that has a 7.05% interest rate that is compounded continuously Part 3: Describe the type of equation that models Sophie’s situation. Create that equation of Sophie’s situation. Using the equation you created, how much money will be in Sophie’s account after 3 years? 10 years?

Answer 1

Sophie

- The formula for continuously compounded interest is given by:

`A=Pe^(rt)`

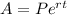
Where:

A is the amount after t years.

P is the principal.

r is the annual interest rate.

Therefore the equation is:

P = $3500

r = 7.05% = 0.0705

`A=3500e^(0.0705t)`

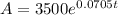
- Money in​ Sophie’s account after 3​ years:

t = 3

`A=3500e^(0.0705(3))=3500e^(0.2115)=4324.35`

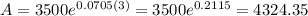
This is $4324.35

- Money in​ Sophie’s account after 10 years:

t = 10

`A=3500e^(0.0705(10))=3500e^(0.705)=7083.46`

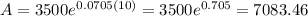
This is $7083.46

Answer

Describe the type of equation that models​ Sophie’s situation: exponential growth model.

Create that equation of​ Sophie’s situation:

`A=3500e^(0.0705t)`

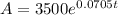
Money will be in​ Sophie’s account after 3​ years: $4324.35

Money will be in Sophie´s account after 10 years: $7083.46