Question

In Young's double-slit experiment, two slits are separated by 5.0 mm and illuminated by light with a wavelength of 480 nm. The screen is 3.0 m from the plane of the slits. Calculate the separation between the eighth bright fringe and the third dark fringe observed with respect to the central bright fringe.

Answer 1

We are given the following information.

Seperation between slits: d = 5.0 mm

Wavelength of light: λ = 480 nm

Distance from the plane of slits: D = 3.0 m

We are asked to calculate the separation between the 8th bright fringe and the 3rd dark fringe observed with respect to the central bright fringe.

The position of the 8th bright fringe is given by

`\begin{gathered} x_n=(n\lambda D)/(d) \\ x_8=(8\cdot480*10^(-9)\cdot3)/(5*10^(-3)) \\ x_8=2.304*10^(-3)\;m \end{gathered}`

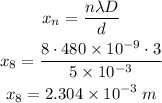
The position of the 3rd dark fringe is given by

`\begin{gathered} x_n=((2n-1)/(2))(\lambda D)/(d) \\ x_3=((2\cdot3-1)/(2))(480*10^(-9)\cdot3)/(5*10^(-3)) \\ x_3=7.2*10^(-4)\;m \end{gathered}`

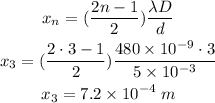
Finally, the separation between the 8th bright fringe and the 3rd dark fringe is

`\begin{gathered} x_8-x_3=2.304*10^(-3)-7.2*10^(-4) \\ x_8-x_3=1.584*10^(-3)\;m \end{gathered}`

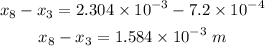
Therefore, the separation between the eighth bright fringe and the third dark fringe observed with respect to the central bright fringe is 1.584×10⁻³ m.