Given:
The equation of the ellipse is,
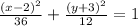
Step-by-step explanation:
The general equation of ellipse with center (h,k) is,
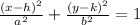
The center of te given ellipse is (2,-3).
Determine the value of a and b.
![\begin{gathered} a=\sqrt[]{36} \\ =6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2r69sg5zttq67yjhaczcgvuyrqo2vpr740.png)
![\begin{gathered} b=\sqrt[]{12} \\ =2\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g2zfx3x86q45c4y9pzwme6a3xw2ojktjdd.png)
The value of a is more than b. so major axis is horiontal and minor axis is vertical.
The coordinates of endpoints of major axis are,
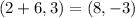
and
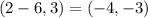
The coordinates of endpoints of minor axis,
![(2,-3+2\sqrt[]{3})](https://img.qammunity.org/2023/formulas/mathematics/college/puioib9hky11n29o8ue02ss3k2j975710w.png)
and
![(2,-3-2\sqrt[]{3})](https://img.qammunity.org/2023/formulas/mathematics/college/lbpxvwzz9m8ae0tt3hnkxmkup54si7bsj2.png)
or we can expressed coordinates of endpoints of minor axis as,
![(2,-3\pm2\sqrt[]{3})](https://img.qammunity.org/2023/formulas/mathematics/college/igqcxbx2ljwzlzz0kw2oliv35w5jvcwhgh.png)