Let x = the number of seats
Let y = the number of rows.
Since the auditorium is rectangular and it has 1,749 people, then we can say that:
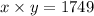
Then, if the number of seats "x" exceeds the number of rows "y" by 20, then we can say that:
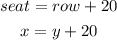
Now we have two equations. To solve for x, let's use the substitution method.
1. Rewrite the equation 2 x = y + 20 into y = x - 20.
2. Replace the value of "y" in equation 1 by x - 20.
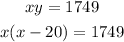
2. Multiply x and x - 20.
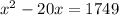
3. Transfer the constant term 1749 on the left side of the equation. When transferring over the equal sign, the operation will change. From +1749, it becomes -1749.

4. To solve this quadratic equation, let's find the factors of -1749 that sums to -20.
a. 3 and -583 = -580
b. 11 and -159 = -148
c. 33 and -53 = -20
As we can see above, the factors of -1749 that sums to -20 are 33 and -53. Hence, the quadratic equation above can be factored to:

5. Equate each factor to zero and solve for x.
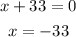
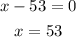
Since the value of x cannot be negative, then the value of x is 53.
Therefore, the number of seats in each row is 53. In addition, there are 33 rows in the auditorium.