whichWe define:
• A = original area = 100 sq units,
,
• A' = dilated area.
If we dilate a trapezoid in a scale factor k, the area scales as:
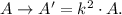
Using the area A = 100 sq units, we have:
![\begin{gathered} A^(\prime)=k^2\cdot100\text{ sq units,} \\ k^2=\frac{A^(\prime)}{100\text{ sq units}}, \\ k=\sqrt[]{\frac{A^(\prime)}{100\text{ sq units}}}\text{.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/rjbx06vj2oarzxpzsv691bta7ut9x1m1uf.png)
This formula gives as the scale factor k for witch we must dilate the trapezoid to have an area A'.
1) For A' = 6400 sq units, we have:
![k=\sqrt[]{\frac{6400\text{ sq units}^{}}{100\text{ sq units}}}=\sqrt[]{64}=8.](https://img.qammunity.org/2023/formulas/mathematics/high-school/ukqrkggpv8kppyewwr2d6wywd5mxc7o26r.png)
2) For A' = 100 sq units, we have:
![k=\sqrt[]{\frac{100\text{ sq units}^{}}{100\text{ sq units}}}=\sqrt[]{1}=1.](https://img.qammunity.org/2023/formulas/mathematics/high-school/hd6g2v7mk4ojh54m5u1ytdgh0mpcrd3h9x.png)
3) For A' = 25 sq units, we have:
![k=\sqrt[]{\frac{25\text{ sq units}^{}}{100\text{ sq units}}}=\sqrt[]{(1)/(4)}=(1)/(2).](https://img.qammunity.org/2023/formulas/mathematics/high-school/36zrremeh0dfde4hznij84c5c0ptigifks.png)
4) For A' = 900 sq units, we have:
![k=\sqrt[]{\frac{900\text{ sq units}^{}}{100\text{ sq units}}}=\sqrt[]{9}=3.](https://img.qammunity.org/2023/formulas/mathematics/high-school/5rp5mq5lg9cho7bnei4wry7o86a6o4e1x9.png)
Answers
• 8
,
• 1
,
• 1/2
,
• 3