Question

Four masses are arranged as shown. They are connected by rigid, massless rods of lengths 0.780 m and 0.500 m. What torque must be applied to cause an angular acceleration of 0.750 rad/s2 about the axis shown?

Answer 1

Given,

The length of the rods;

L=0.780 m

l=0.500 m

The angular acceleration, α=0.750 rad/s²

The masses;

m_A=4.00 kg

m_B=3.00 kg

m_C=5.00 kg

m_D=2.00 kg

The moment of inertia of the given system of masses is given by,

`\begin{gathered} I=\Sigma mr^2 \\ =m_A((L)/(2))^2+m_B((L)/(2))^2+m_C((L)/(2))^2+m_D((L)/(2))^2 \\ =((L)/(2))^2(m_A+m_B+m_C+m_D) \end{gathered}`

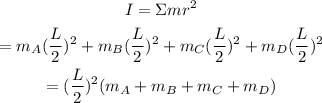
Where r is the distance between each mass and the axis of rotation.

On substituting the known values,

`\begin{gathered} I=((0.780)/(2))^2(4.00+3.00+5.00+2.00) \\ =2.13\text{ kg}\cdot\text{m}^2 \end{gathered}`

The torque required is given by,

`\tau=I\alpha`

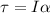
On substituting the known values,

`\begin{gathered} \tau=2.13*0.750 \\ =1.6\text{ Nm} \end{gathered}`

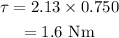
Thus the torque that must be applied to cause the required acceleration is 1.6 Nm