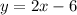Question

What is the equation of the line that is parallel to the graph of y = 2x - 5 and passes through the point (8, 10)?

Answer 1

We know that the equation of a line is given by

`y-y_1=m(x-x_1)`

To find it we need the slope m and a point that the line passes thorugh. In this case we have the point (8,10) but we don't know the slope. What we know is that the line we are looking for is parallel to the line

`y=2x-5`

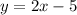
We also know that for two lines to be parallel they have the same slope. Then, if we fin the slope of the line y=2x-5, we have the slope of the line we are looking for. To find the slope of the line y=2x-5 we note that it is written in the slope-intercept form

`y=mx+b`

From this we know that the slope is multiplying the x variable when it is written in that form. Hence m=2.

Then the line we are looking for has an slope of 2 and passes through the point (8,10). Pluggin the values in the equation of a line we have.

`y-10=2(x-8)`

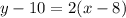
Writting it in the slope intercept form we have

`\begin{gathered} y-10=2(x-8) \\ y-10=2x-16 \\ y=2x-16+10 \\ y=2x-6 \end{gathered}`

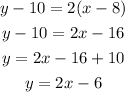
Then the line parallel to y=2x-5 and passes through the point (8,10) is

`y=2x-6`