Question

A population of bacteria grows according to function p(t) = p. 1.42^t, where t is measured in hours. If the initial population size was1,000 cells, approximately how long will it take the population to exceed 10,000 cells? Round your answer to the nearest tenth.

Answer 1

Given the function p(t) and the initial condition, we have the following:

`\begin{gathered} p(t)=p_0\cdot1.42^t \\ p(0)=1000 \\ \Rightarrow p(0)=p_0\cdot1.42^0=1000 \\ \Rightarrow p_0\cdot1=1000 \\ p_0=1000 \end{gathered}`

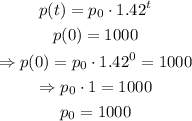
Therefore, the function p(t) is defined like this:

`p(t)=1000\cdot1.42^t`

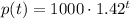
Now, since we want to know the time it will take the population to exceed 10,000 cells, we have to solve for t using this information like this:

`\begin{gathered} p(t)=1000\cdot1.42^t=10000 \\ \Rightarrow1.42^t=(10000)/(1000)=10 \\ \Rightarrow1.42^t=10 \end{gathered}`

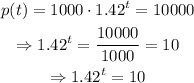
Applying natural logarithm in both sides of the equation we get:

`\begin{gathered} 1.42^t=10 \\ \Rightarrow\ln (1.42^t)=\ln (10) \\ \Rightarrow t\cdot\ln (1.42)=\ln (10) \\ \Rightarrow t=(ln(10))/(\ln (1.42))=6.56 \end{gathered}`

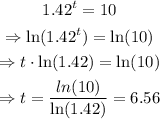
Therefore, it will take the population 6.56 hours to exceed 10,000 cells