Step-by-step explanation
To begin with, we will first have to obtain the length of side VX
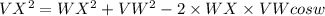
In our case
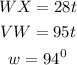
Thus
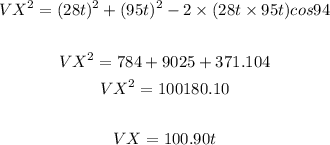
Next, we will determine the angles at V and X
using sine rule
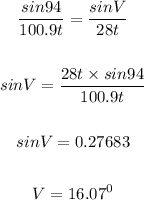
Then, we will get the measure at X
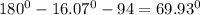
Therefore, the order from smallest to largest angles will be
m
OR
m