Question

-Quadratic Equations- Solve each by factoring, write each equation in standard form first.

Answer 1

The solutions to the quadratic equations are

`\begin{gathered} a^2-4a-45 \\ \text{Solution: }a=-5\text{ or }9 \\ \\ 5y^2+4y=0 \\ \text{Solution: }y=0\text{ or }-(4)/(5) \end{gathered}`

SOLUTION

Problem Statement

The question gives us 2 quadratic equations and we are required to solve them by factoring, first writing them in their standard forms.

The quadratic equations given are:

`\begin{gathered} a^2-4a-45=0 \\ 5y^2+4y=0 \end{gathered}`

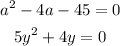
Method

To solve the questions, we need to follow these steps:

(We will represent the independent variable as x for this explanation. We know they are "a" and "y" in the questions given)

The steps outlined below are known as the method of Completing the Square.

Step 1: Find the square of the half of the coefficient of x.

Step 2: Add and subtract the result from step 1.

Step 3: Re-write the Equation. This will be the standard form of the equation

Step 4. Solve for x

We will apply these steps to solve both questions.

Implementation

Question 1:

`\begin{gathered} a^2-4a-45=0 \\ \text{Step 1: Find the square of the half of the coefficient of }a \\ (-(4)/(2))^2=(-2)^2=4 \\ \\ \text{Step 2: Add and subtract 4 to the equation} \\ a^2-4a-45+4-4=0 \\ \\ \text{Step 3: Rewrite the Equation} \\ a^2-4a+4-45-4=0 \\ (a^2-4a+4)-49=0 \\ (a^2-4a+4)=(a-2)^2 \\ \therefore(a-2)^2-49=0 \\ \text{ In standard form, we have:} \\ (a-2)^2=49 \\ \\ \text{Step 4: Solve for }a \\ (a-2)^2=49 \\ \text{ Find the square root of both sides} \\ \sqrt[]{(a-2)^2}=\pm\sqrt[]{49} \\ a-2=\pm7 \\ \text{Add 2 to both sides} \\ \therefore a=2\pm7 \\ \\ \therefore a=-5\text{ or }9 \end{gathered}`

Question 2:

Final Answer

The solutions to the quadratic equations are

`\begin{gathered} a^2-4a-45 \\ \text{Solution: }a=-5\text{ or }9 \\ \\ 5y^2+4y=0 \\ \text{Solution: }y=0\text{ or }-(4)/(5) \end{gathered}`