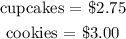Answer:
The cost of cupcakes and cookies are;
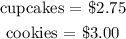
Step-by-step explanation:
Let x and y represent the cost of a cupcake and cookie respectively.
Given that;
Five cupcakes and two cookies cost $19.75.

Two cupcakes and four cookies cost $17.50.
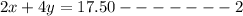
Let's solve the simultaneous equation by elimination;
multiply equation 1 by 2;
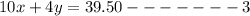
subtract equation 2 from equation 3;
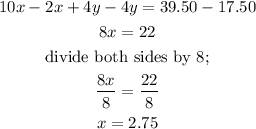
since we have the value of x, let substitute into equation 1 to get y;
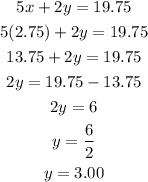
Therefore, the cost of cupcakes and cookies are;