From the information provided, the lawn mower is sold at a price which is $75 over the cost of manufacture.
If the cost of manufacture is x, then we would have;
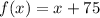
Also, the store now sells the lawn mower for 140% of the price paid to the manufacturer. Therefore, we would have;
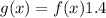
Hence, if the manufacturer's cost is $230, the customer would be paying g(x). When the cost x is now given as 230, we wou;d have;
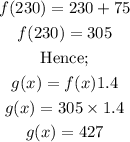
ANSWER:
The function of the price is;
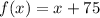
The price a customer pays when the cost of manufacturing is $230 would now be $427