Question

Which 3 pairs of side lengths are possible measurements for the triangle?

Answer 1

From the right triangle with two interior angles of 45 degrees, the two legs are equal in length, that is AB = BC

And from Pythagoras, the square of the hypotenuse (AC) is equal to the square of the other two legs or sides (AB and AC)

So this means

`\begin{gathered} |AC|^2=|AB|^2+|BC|^2 \\ since\text{ AB = BC} \\ |AC|^2=2|AB|^2,\text{ also } \\ |AC|^2=2|BC|^2 \end{gathered}`

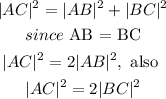
So from the first option

`\begin{gathered} BC=10,AC=10√(2) \\ |AC|^2=(10√(2))^2=100*2=200 \\ 2|BC|^2=2*10^2=2*100=200 \end{gathered}`

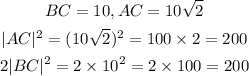
Hence the 1st option is correct, so its possible

The second option

`\begin{gathered} AB=9,AC=18 \\ |AC|^2=18^2=324 \\ 2|AB|^2=2*9^2=2*81=162 \\ 324\\e162 \end{gathered}`

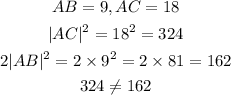
Hence the 2nd option is wrong, hence not possible

The 3rd option

`\begin{gathered} BC=10√(3),AC=20 \\ |AC|^2=20^2=400 \\ 2|BC|^2=2*(10√(3))^2=2*100*3=600 \\ 400\\e600 \end{gathered}`

Hence the 3rd option is wrong, not possible

The 4th option

`\begin{gathered} AB=9√(2),AC=18 \\ |AC|^2=18^2=324 \\ 2|AB|^2=2*(9√(2))^2=2*81*2=324 \\ 324=324 \end{gathered}`

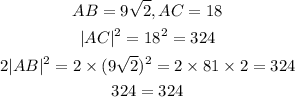
Hence the 4th option is correct, it is possible

The 5th option

AB = BC

This is correct, and its possible

The last option

`\begin{gathered} AB=7,BC=7√(3) \\ 7\\e7√(3) \end{gathered}`

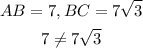
This is wrong and not possible because AB should be equal to BC

Hence the correct options are the options bolded, which are

1st, 4th and 5th