Answer:
a) r = 0.79%
b)
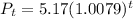
c) 6.6 million people
d) 2046
Step-by-step explanation:
We'll use the below formula for exponential growth;
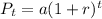
where a = initial amount
r = growth rate
t = number of time intervals
a) From the question, we have that
a = 5.17 million
P(t)= 6.05 million
t = 20 years
Let's go ahead and substitute these values into our formula, and solve for r as shown below;
![\begin{gathered} 6.05=5.17(1+r)^(20) \\ (6.05)/(5.17)=(1+r)^(20) \\ (1+r)=\sqrt[20]{(6.05)/(5.17)} \\ r=\sqrt[20]{(6.05)/(5.17)}-1 \\ r=0.00789 \\ r=0.79\text{\%} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1243f99fqaq3ana1e42ek1fpsa4e5udoks.png)
b) The exponential model can be written as shown below;
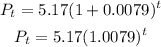
c) When t = 31 years, let's go ahead and find P as shown below;
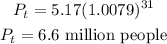
d) When P = 7.5 million, let's go ahead and solve for t as shown below;
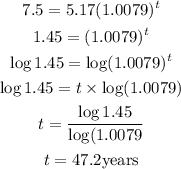
So to get the particular year all we need to do is add 47 years to the initial year. That will us 1999 + 47 = 2046