Answer
A = 46.3°
B = 75.7°
c = 3.5
Step-by-step explanation
We will be using both Cosine and Sine rule to solve this.
For Cosine rule,
If a triangle ABC has angles A, B and C at the points of the named vertices of the tringles with the sides facing each of these angles tagged a, b and c respectively, the Cosine rule is given as
c² = a² + b² - 2ab Cos C
a = 3.0
b = 4.0
C = 58°
c² = 3² + 4² - 2(3)(4)(Cos 58°)
c² = 9 + 16 - (24)(0.5299)
c² = 25 - 12.72 = 12.28
c = √12.28 = 3.50
To find the other angles, we will now use Sine Rule
If a triangle ABC has angles A, B and C at the points of the named vertices of the tringles with the sides facing each of these angles tagged a, b and c respectively, the sine rule is given as
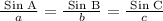
So, we can use the latter parts to solve this
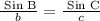
B = ?
b = 4.0
C = 58°
c = 3.5

We can then solve for Angle A
The sum of angles in a triangle is 180°
A + B + C = 180°
A + 75.7° + 58° = 180°
A = 180° - 133.7° = 46.3°
Hope this Helps!!!