Question

Find the percent increase in volume when 1 foot is added to each dimension of the prism. Round your answer to the nearest tenth of a percent.7 ft10 ft86 ft

Answer 1

Step 1

The volume of a triangular prism = Cross-sectional area x Length

Step 2

`\begin{gathered} Cross\text{ sectional area = area of the triangle} \\ Base\text{ = 6ft} \\ Height\text{ = 7ft} \\ Cross\text{ sectional area = }(1)/(2)*\text{ 7 }*\text{ 6 = 21 ft}^2 \\ Volume\text{ = 21 }*\text{ 10 = 210 ft}^3 \end{gathered}`

Step 3:

When 1 foot is added to each dimension of the prism.

The new dimensions becomes Base = 7, Height = 8 and length = 11

`\begin{gathered} \text{Cross-sectional area = }(1)/(2)\text{ }*\text{ 7 }*\text{ 8 = 28 ft}^2 \\ Length\text{ = 11 ft} \\ Volume\text{ = 28 }*\text{ 11 = 308 ft}^3 \end{gathered}`

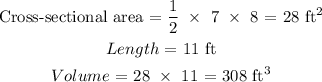
Step 4

Find the percent increase in volume

`\begin{gathered} \text{Percent increase in volume = }\frac{308\text{ - 210}}{210}\text{ }*\text{ 100\%} \\ \text{= }(98)/(210)\text{ }*100 \\ \text{= 46.7} \end{gathered}`

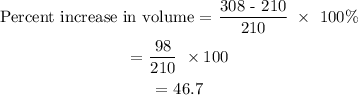
Final answer

46.7