8 dlls for silver
16 dlls for brass
5 dlls profit silver
7 dlls profit spheres
Then the price is
8+5= 13 dlls for silver
16+7=23 dlls for brass
Let S and B be the amount of magnetic silver and brass sphers that are sold, respectively.
Then, Ms. Ball estimation is that

Also, she doesn't want to invest more than 20000, so
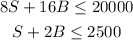
The objective function is
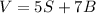
Subjected to:
GRAPH
The interection is at
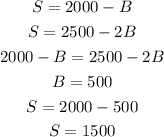
So, the extremes must be at (0,1250), (1500,500), (2000,0) , (0,0).
So, if we replace the points
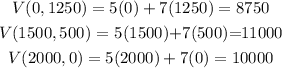
So, the amount she will need to stock to maximize her profit is 1500 of silver and 500 of brass, and the maximum profit is going to be 11000 dlls.