Question

How do I solve it and what would be the answer

Answer 1

The quotient is x² + 4x + 3

Yes, (x - 2) is a factor of x³ + 2x² - 5x - 6

Step-by-step explanation: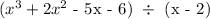
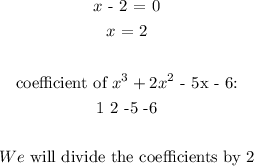
`(x^3+2x^2\text{ - 5x - 6) }/\text{ (x - 2)}`
`\begin{gathered} x\text{ - 2 = 0} \\ x\text{ = 2} \\ \\ \text{coefficient of }x^3+2x^2\text{ - 5x - 6:} \\ 1\text{ 2 -5 -6} \\ \\ We\text{ will divide the coefficients by 2} \end{gathered}`

Using synthetic division:

`\begin{gathered} (x^3+2x^2\text{ - 5x - 6) }/\text{ (x - 2) = }\frac{(x^3+2x^2\text{ - 5x - 6)}}{\text{(x - 2)}} \\ \frac{(x^3+2x^2\text{ - 5x - 6)}}{\text{(x - 2)}}\text{ = quotient + }\frac{remai\text{ nder}}{\text{divisor}} \\ \\ The\text{ coefficient of the quotient = 1 4 3} \\ \text{The last number is zero, so the remainder = 0} \end{gathered}`
`\begin{gathered} \frac{(x^3+2x^2\text{ - 5x - 6)}}{\text{(x - 2)}}=1x^2\text{ + 4x + 3 + }\frac{0}{x\text{ - 2}} \\ \text{quotient }=\text{ }x^2\text{ + 4x + 3} \end{gathered}`

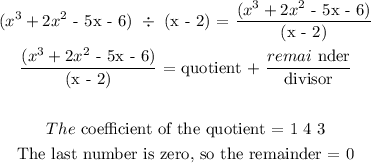
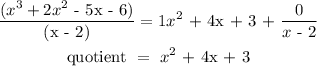
For a (x - 2) to be a factor of x³ + 2x² - 5x - 6, it will not have a remainder when it is divided.

Since remainder = 0

Yes, (x - 2) is a factor of x³ + 2x² - 5x - 6