The sample size given in the question is
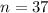
The mean weight is
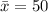
The standard deviation is
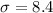
The margin of error is calculated using the formula below
![\text{MOE = Z-score(90\% C.I)}*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/6dfv08aitzpvehg5npd9g8zs12rul36mnw.png)
Using the Z-score table, the Z-score for the 90% confidence interval is
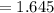
By substituting the values in the formula above, we will have
![\begin{gathered} \text{MOE = Z-score(90\% C.I)}*\frac{\sigma}{\sqrt[]{n}} \\ \text{Margin of error(MOE)} \\ =1.645*\frac{8.4}{\sqrt[]{37}} \\ =\frac{13.818}{\sqrt[]{37}} \\ =\pm2.272\text{ounces} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/fz3vw1p14aja941p59kzrpwfxd8h05z0il.png)
Hence,
The final answer is = ±2.272 ounces