Question

a quadratic function has its vertex at the point (4,6) the function passes through the point (-5,-2) find the quadratic and linear coefficients and the constant term of the function The quadratic coefficient is_____The linear coefficient is_______the constant term is_____

Answer 1

We have to find the equation of the quadratic function.

We know the vertex, located in (4,6), and one point (-5,-2).

The x-coordinate of the vertex (4) is equal to -b/2a, being a the quadratic coefficient and b the linear coefficient.

Now, we have 2 points to define the 3 parameters, so one of the parameters is undefined.

`y=ax^2+bx+c`

We start with the vertex, that we know that is:

`\begin{gathered} x=-(b)/(2a)=4 \\ -b=4\cdot2a=8a \\ b=-8a \end{gathered}`

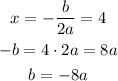
Then, we can write the equation as:

`y=ax^2-8ax+c=a(x^2-8x)+c`

If we replace the point (-5,-2) in the equation, we get:

`\begin{gathered} -2=a((-5)^2-8\cdot(-5))+c \\ -2=a(25+40)+c \\ -2=65a+c \\ c=-2-65a \end{gathered}`

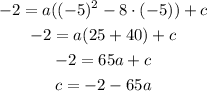
We replace the vertex coordinates and get:

`\begin{gathered} 6=a(4^2-8\cdot4)+c \\ 6=a(16-32)+(-2-65a) \\ 6=-16a-2-65a \\ 6=-81a-2 \\ 81a=-2-6 \\ a=-(8)/(81)\approx-0.01 \end{gathered}`

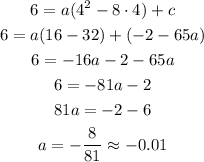
Then, the linear coefficient b is:

`b=-8a=-8\cdot(-(8)/(81))=(64)/(81)\approx0.79`

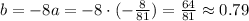
And the constant term is:

`c=-2-65a=-2-65\cdot(-(8)/(81))=-2+(520)/(81)=(-162+520)/(81)=(358)/(81)\approx4.42`

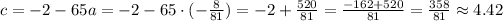
The quadratic coefficient is a=-0.01

The linear coefficient is b=0.79

the constant term is c=4.42