Question

11. The population of the District of Columbia was approximately 572 thousand in 2000 and had been growing by about 1.15% per year.(a) Write an explicit formula for the population of DC t years after 2000 (i.e. t=0 in 2000), where Pt is measured in thousands of people.Pt = (b) If this trend continues, what will the district's population be in 2025? Round your answer to the nearest whole number. thousand people(c) When does this model predict DC's population to exceed 800 thousand? Give your answer as a calendar year (ex: 2000).During the year

Answer 1

Given:

Population in 2000 = 572 thousand

Rate of growth per year = 1.15%

Let's solve for the following:

(a) Explicit formula for the population years after 2000.

Where:

In year 2000, t = 0

To write the explicit formula, apply the exponantial growth function formula:

`f(t)=a(1+r)^t`

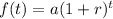
Where:

a is the initial amount

r is the growth rate.

Thus, we have:

`\begin{gathered} P_t=572(1+(1.15)/(100)_{^{}})^t \\ \\ P_t=572(1+0.0115)^t \end{gathered}`

Therefore, the explicit formula for the population years after 2000 is:

`P_t=572(1.0115)^t`

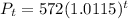
(b) What will be the district's population in 2025.

Where:

In the year 2000, t = 0

In the year 2025, t will be = 25

To find the population in 2025, substitute 25 for t in the explicit formula for evalaute:

`\begin{gathered} P_(25)=572(1.0115)^(25) \\ \\ P_(25)=572(1.330905371) \\ \\ P_(25)=761.28\approx761 \end{gathered}`

The population in 2025 if the trend continues will be approximately 761 thousand.

(c) When does the model predict the population to exceeed 800 thousand.

Substitute 800 for Pt and solve for t.

We have:

`\begin{gathered} P_t=572(1.0115)^t \\ \\ 800=572(1.0115)^t \end{gathered}`

Divide both sides by 572:

`\begin{gathered} \frac{800}{572^{}}=(572(1.0115)^t)/(572) \\ \\ 1.3986=1.0115^t \end{gathered}`

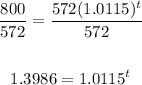
Take the natural logarithm of both sides:

`\begin{gathered} \ln (1.3986)=\ln (1.0115)^t \\ \\ \ln (1.3986)=t\ln (1.0115) \\ \\ 0.33547=0.01143t \end{gathered}`

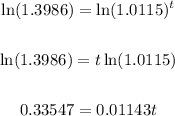
Divide both sides by 0.01143:

`\begin{gathered} (0.33547)/(0.01143)=(0.01143t)/(0.01143) \\ \\ 29.3=t \\ \\ t=29.3\approx29 \end{gathered}`

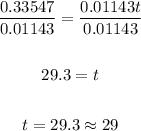
When t = 29, the year is 2000 + 29 = 2029

Therefore, using this model, DC's population will exceed 800 thousand in the year 2029.

ANSWERS:

`\begin{gathered} (a)P_t=572(1.0115)^t \\ \\ (b)=761\text{ thousand people} \\ \\ (c)\text{ 20}29 \end{gathered}`