Solution
Given that
Area f small square = 40 inches squared.
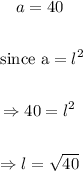
Let the side of the large square be L
Since the large square has sides that are 8 times longer than the small square
=> L = 8l
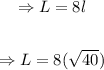
Hence, the area of Large square is;
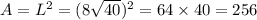
Hence, the area of the large square is: 256 inches squared.