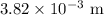We know that the wavelength is related to the speed of the wave by:
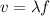
where f is the frequency.
The speed of sound on air at a given temperature is given by:
![v=331\sqrt[]{1+(T)/(273)}](https://img.qammunity.org/2023/formulas/physics/college/dx7fgpct0wcibxzocg0d9sz3ou1pe6ziax.png)
so in this case the speed is:
![v=331\sqrt[]{1+(22)/(273)}=344.08](https://img.qammunity.org/2023/formulas/physics/college/s6n8rodbkkxhuycgzhhu9mo5ldwgmmmfhh.png)
Plugging this and the frequency in the first expression above we have:
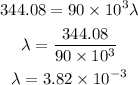
Therefore the wavelength is: