Question

Tom Blasting invested $4,500 in an investment paying 10% compounded quarterly for 3 years. Find the interest

Answer 1

Given that Tom invested $4500 in an investment paying 10% compounded quarterly for 3 years.

We have to find the interest for the given time period.

We know that the formula of amount on a principal P, rate r per annum, time t years where interest is compounding quarterly is:

`A=P(1+(r)/(4))^(4t)`

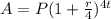
Here, P = 4500, r = 0.1 and t = 3. So,

`\begin{gathered} A=4500(1+(0.1)/(4))^(4(3)) \\ =4500(1+0.025)^(12) \\ =4500(1.025)^(12) \\ =4500(1.3448) \\ =6051.6 \end{gathered}`

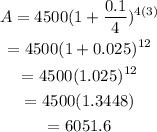
So, the amount we get is $6051.6.

Now, it is known that the interest is the difference between the amount and the principal. So,

`\begin{gathered} \text{ interest}=\text{ amount-principal} \\ =6051.6-4500 \\ =1551.6 \end{gathered}`

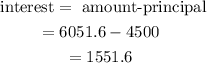
Thus, the interest is $1551.6.