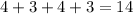Question

The perimeter of a rectangular poster is 14 feet and the length is 4 feet. Describe how to use the perimeter formula to find the width.This calculator has a tray why the answer is not 3.2

Answer 1

Step-by-step explanation

We are told that the perimeter of a rectangular poster is 14 feet and the length is 4 feet.

Perimeter simply means the total sum of all the sides of the rectangle

`\begin{gathered} From\text{ the above} \\ let\text{ the length = y} \\ width\text{ =x} \end{gathered}`

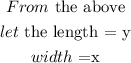
So, the perimeter is

`x+x+y+y=2x+2y`

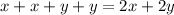
Since the perimeter is 14 then

`2x+2y=14`

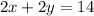
Also, the length is 4 feet

Therefore y = 4, so that

`\begin{gathered} 2x+2(4)=14 \\ 2x+8=14 \\ collecting\text{ like terms} \\ 2x=14-8 \\ 2x=6 \end{gathered}`

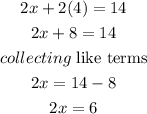
Making x the subject of the formula

`\begin{gathered} x=(6)/(2)=3 \\ \\ x=3 \end{gathered}`

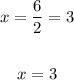
Therefore, the width of the rectangle is 3 feet

The rectangle is

`4+3+4+3=14`