Question

A hot air balloon was descending at a rate of 25 feet per minute and was known to be at an altitude of 425 feet above the ground 21 minutes after it began its descenta) determine the slope-intercept form of the equationb) How high was the balloon when it began its descent (0 minutes)c) How many minutes did it take to land?

Answer 1

We can model the problem as a linear equation of the form:

`y=mx+b`

Where:

m = Slope (Rate of change)

b = y-intercept (Initial value)

a)

Since it is descending at a rate of 25ft per minute, the slope is:

`m=-25`

So, the equation is:

`y=-25x+b`

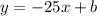
b) We know that the ballon was 425ft above the ground 21 minutes after it began its descent, so:

`\begin{gathered} y=425,x=21 \\ so\colon \\ 425=-25(21)+b \\ 425=-525+b \\ b=950 \end{gathered}`

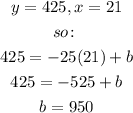
Therefore, the balloon was 950ft when it began its descent, so, we can conclude that the y-intercept is 950, now the equation is complete

`y=-25x+950`

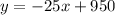
c) We need to know for which value of x, y is equal to 0, so:

`\begin{gathered} y=0 \\ 0=-25x+950 \end{gathered}`

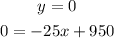
Solve for x:

`\begin{gathered} 25x=950 \\ x=(950)/(25) \\ x=38 \end{gathered}`

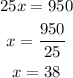
The balloon will land after 38 minutes