Note that the lateral surface area is the area of the faces of the solid, excluding the cross-sectional faces i.e. faces which are perpendicular to the longitudinal axis.
The lateral surface area of prism A is calculated as,
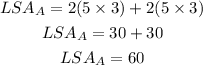
Similarly, the lateral surface area of prism A is calculated as,
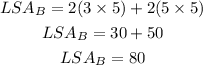
Clearly, prisms A and B have different values of lateral surface area.
So option A is the correct statement.
The total surface area is the sum of all the faces of the solid.
Since we have already calculated the LSA i.e. sum of area of 4 faces of the prism, we can add the area of the two remaining cross sectional faces to get the total area.
The total cross section area of prism B is calculated as,
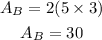
So the total surface area of prism B becomes,
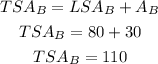
The total surface area of prism B is 110 sq. cm.
So option B is also correct.
Note that we have already found that the lateral surface area of prism A is 60 sq. cm.
Therefore, option C is also correct.
The total cross section area of prism A is calculated as,
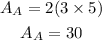
So the total surface area of prism A becomes,
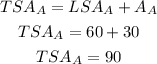
The total surface area of prism A is 90 sq. cm.
It is oberved that prism B has a larger surface area.
So, option D is also correct.
Hence, we can conclude that all the given statements are correct.