We want to create a real-life reasonable problem in which we can apply the laws of exponents.
Using a compound interest example;
Word Problem:
Calculate the final value of a $2,000 investment in an account with a 5% interest compounded Quarterly for 5 years.
Solving the word problem;
We have the following parameters;
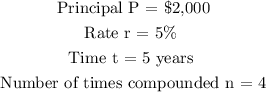
Recall that the formula for compound interest is;
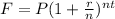
Substituting the given values;
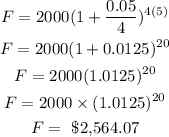
Therefore, the solution to the problem is;
The final