We are asked to determine the sinT. To do that let's remember that the function sine is defined as:
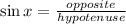
In this case, we have:

To determine the value of VU we can use the Pythagorean theorem which in this case would be:

Now we solve for VU first by subtracting TU squared from both sides:
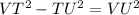
Now we take the square root to both sides:
![\sqrt[]{VT^2-TU^2^{}}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/p35n9ptnlqkai0f5xtnfcj9dexdkpxuume.png)
Now we plug in the values:
![\sqrt[]{(6)^2+(\sqrt[]{36^{}})^2}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/c5tqam7megy63nq040x4xi54lwrtvdiqgi.png)
Solving the squares:
![\sqrt[]{36+36}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/d9d0xda6l8br41ubojavdnwojxu0qfchgh.png)
Adding the values:
![\sqrt[]{2(36)}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/ouo06pgc7nfon13upww2puqn8o7y1pwpqj.png)
Now we separate the square root:
![\sqrt[]{2}\sqrt[]{36}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/gcdzfz1to78vvx8wjcwsyuo1f4fzx3pah0.png)
Solving the square root:
![6\sqrt[]{2}=VU](https://img.qammunity.org/2023/formulas/mathematics/college/whbze7hk0fcpozaewjpu92ppl69olv2g7a.png)
Now we plug in the values in the expression for sinT:
![\sin T=\frac{6\sqrt[]{2}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/sl8u74kc23p50popce5wtyi6ul5wj352hl.png)
Now we simplify by canceling out the 6:
![\sin T=\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/jdnbwbyqo3qhph7stya79z8vuumw9xr7uk.png)
And thus we obtained the expression for sinT.