Question

Look at the expression below.2h + y 4h^2_______ - _____9h^2-y^2 3h+yWhich of the following is the least common denominator for the expression?

Answer 1

(3h+y)*(3h-y)

Explanation:

We are given the following expression:

`(2h+y)/(9h^2-y^2)-(4h^2)/(3h+y)`

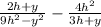
We want to find the LCD for:

9h²-y² and 3h + y.

3h+y is already in it's most simplified way.

9h²-y² , according to the notable product of (a²-b²) = (a-b)*(a+b), can be factored as:

(3h-y)*(3h+y).

The factors of each polynomial is:

3h + y and (3h-y)*(3h+y)

The LCD uses all unique factors(If a factor is present in more than one polynomial, it only appears once).

So the LCD is:

(3h+y)*(3h-y)

Which is option B.