Given the function:
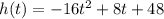
Where h(t) is the height of the diver above the surface of the water and t is the time.
Let's find how long it takes the diver to hit the water.
When the diver hits the water, the height h(t) = 0.
Now substitute 0 for h(t) and solve for the time t.
We have:
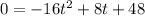
Rearrange the equation:
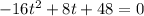
Solve for t.
Let's factor the expression by the left.
Factor 8 out of all terms:
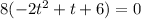
Now, factor by grouping.
Rewrite the middle term as a sum of two terms whose product is the product of the first term and the last term:
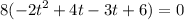
Solving further:
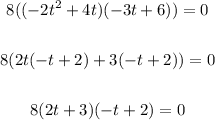
Hence, we have the factors:

Solve each factor for t:

Hence, we have the solutions:
t = -3/2
t = 2
The time cannot be negative, so let's take the positive value.
Therefore, the will take 2 seconds for the diver to hit the water.
ANSWER:
2 seconds.