An exponential function has the form

Therefore, to find an exponential function that satisfies our condition, we need to find a and b.
From f(-2) = 1, we have
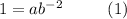
and from f(7) = 63, we have

Solving for a in equation (1) gives
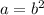
substituting this value of a into equation (2) gives
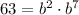
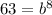
![\begin{gathered} \therefore b=\sqrt[8]{63} \\ b=1.6785 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/xn6cx5vepu769p4p0k4akvtjyqt4fb0ct6.png)
With the value of b in hand, we now find the value of a:
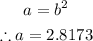
Hence, the exponential function is
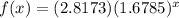
Evaluating the above function at x = 1 gives
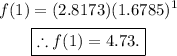
which is our answer!