To obtain the measure of segment AD, add the measurement of segment AC and segment CD.
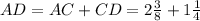
Rewrite the fraction part as similar fractions. Multiply the numerator and teh denominator of the second fraction by 2 to obtain 8 in the denominator.
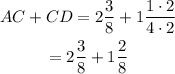
Add the whole numbers, 2 and 1. Add the numerators, 3 and 2, and then copy the common denominator, which is 8.

Therefore, the correct answer is the third option, 3 5/8 in.