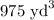Answer:
To find the volume of the cone rounded to the nearest tenth
we have that,
Volume of the cone (V) is,
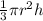
where r is the radius and h is the height of the cone.
Given that,
r=7 yd
h=19 yd
Substitute the values we get,

we get,
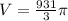
we know that pi is approximately equal to 3.14, Substitute the value we get,
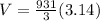
we get,
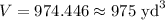
Answer is: Option D: