Question

I need to find the equation of a circle I will include picture

Answer 1

Given,

The center of the circle is (6, -3).

The coordinates of the point, circle is passing through (6,6).

The general equation of the circle is,

`(x-h)^2+(y-k)^2=r^2`

Here, x, y are the coordinates of the point.

h and k are the center of the circle.

r is the radius of the circle.

Substituting the value of h, k , x and y in the equation of circle then,

`\begin{gathered} (6-6)^2+(6-(-3))^2=r^2 \\ 0+9^2=r^2 \\ r=9 \end{gathered}`

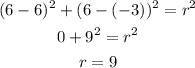
So, the radius of the circle is 9.

Substituting the value of h, k and r in the general equation of circle.

`\begin{gathered} (x-6)^2+(y-(-3))^2=9^2 \\ x^2+36-12x+y^2+9+6y=81 \\ x^2+y^2-12x+6y-36=0 \end{gathered}`

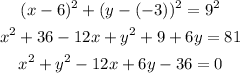
Hence, the equation of circle is x^2+y^2-12x+6y-36=0