Question

random variables, probability distributions and expected value Alyssa likes to play roulette, but she doesn't like the low probability of betting on a single number. Therefore, she bets on a block of 4 numbers, increasing her probability of winning to 38. She generally places a $5 chip on her block of 4. If any other number comes up she loses her bet, but if one of her 4 numbers come up, she wins $40 (and gets to keep her bet!). What is the expected value for Alyssa playing roulette? Round to the nearest cent. Do not round until your final calculation.

Answer 1

We have to calculate the expected value for Alyssa playing roulette.

The expected value is calculated as the weighted sum of all the possible the outcomes, weighted by the probabilities of occurrence of this outcomes.

Then, we start by listing all the outcomes:

1) One of the numbers of the block comes up.

This will happen with a probability of 4 out of 38 (P=4/38). NOTE: The total numbers of the roulette are 38.

The net prize, that is excluding the $5 she bets, is $40.

2) None of the numbers of the block comes up.

That will happen with probability 34 out of 38 (P=34/38).

The net prize, as she will lose the $5 she bets, is -$5.

The expected value can be calculated as:

`E=\sum ^2_(i=1)p_i\cdot X_i=(4)/(38)\cdot40+(34)/(38)\cdot(-5)=(160)/(38)-(170)/(38)=(-10)/(38)\approx-0.26`

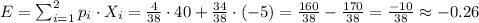
The expected value for Alyssa is -$0.26.