Question

5.Given the sample triangle below and the conditions a=3, c = _51, find:cot(A).

Answer 1

Trigonometry

STEP 1: naming the sides of the triangle

Depending on the angle we are analyzing on the right triangle, each side of it takes a different name. In this case, we are going to name them depending on the angle A. Then,

a: opposite side (to A)

b: adjacent side

c: hypotenuse

STEP 2: formula for cot(A)

We know that the formula for cot(A) is:

`\cot (A)=\frac{\text{adjacent}}{\text{opposite}}`

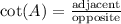
Replacing it with a and b:

`\begin{gathered} \cot (A)=\frac{\text{adjacent}}{\text{opposite}} \\ \downarrow \\ \cot (A)=(b)/(a) \end{gathered}`

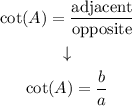
Since a = 3:

`\cot (A)=(b)/(3)`

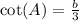
STEP 3: finding b

We have an expression for cot(A) but we do not know its exact value yet. First we have to find the value of b to find it out.

We do this using the Pythagorean Theorem. Its formula is given by the equation:

`c^2=a^2+b^2`

Since

a = 3

and

c = √51

Then,

`\begin{gathered} c^2=a^2+b^2 \\ \downarrow \\ \sqrt[]{51}^2=3^2+b^2 \\ 51=9+b^2 \end{gathered}`

solving the equation for b:

`\begin{gathered} 51=9+b^2 \\ \downarrow\text{ taking 9 to the left} \\ 51-9=b^2 \\ 42=b^2 \\ \downarrow square\text{ root of both sides} \\ √(42)=√(b^2)=b \\ \sqrt[]{42}=b \end{gathered}`

Then,

b= √42

Therefore, the equation for cot(A) is:

`\begin{gathered} \cot (A)=(b)/(3) \\ \downarrow \\ \cot (A)=\frac{\sqrt[]{42}}{3} \end{gathered}`

Answer: D