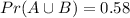Given: A and B are two sets such that-
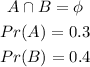
Required: To determine-
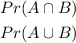
Explanation: Since A and B have no common elements, the events are independent events or disjoints or mutually exclusive.
For independent events, we have-
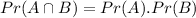
Substituting the values into the formula-
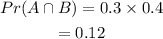
Recall that-
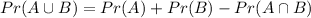
Substituting the values into the formula and further solving as-
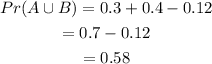
Final Answer: a)
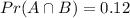
b)