Question

What does the slower car travel at Then what does the faster car travel at

Answer 1

Given that two cars are 188 miles apart, travelling at different speeds, meet after two hours.

To Determine: The speed of both cars if the faster car is 8 miles per hour faster than the slower car

Solution:

Let the slower car has a speed of S₁ and the faster car has a speed of S₂. If the faster speed is 8 miles per hour faster than the slower car, then,

`S_2=8+S_1====\text{equation 1}`

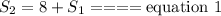
It should be noted that the distance traveled is the product of speed and time. Then, the total distance traveled by each of the cars before they met after 2 hours would be

`\begin{gathered} \text{distance}=\text{speed }* time \\ \text{Distance traveled by the faster car after 2 hours is} \\ =S_2*2=2S_2 \\ \text{Distance traveled by the slower car after 2 hours is} \\ =S_1*2=2S_1 \end{gathered}`

It was given that the distance between the faster and the slower cars is 188 miles. Then, the total distance traveled by the two cars when they meet is 188 miles.

Therefore:

`\begin{gathered} \text{Total distance traveled by the two cars is} \\ 2S_1+2S_2=188====\text{equation 2} \end{gathered}`

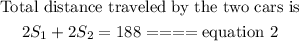
Combining equation 1 and equation 2

`\begin{gathered} S_2=8+S_1====\text{equation 1} \\ 2S_1+2S_2=188====\text{equation 2} \end{gathered}`

Substitute equation 1 into equation 2

`\begin{gathered} 2S_1+2(8+S_1)=188 \\ 2S_1+16+2S_1=188 \\ 2S_1+2S_1=188-16 \\ 4S_1=172 \end{gathered}`

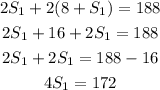
Divide through by 4

`\begin{gathered} (4S_1)/(4)=(172)/(4) \\ S_1=43 \end{gathered}`

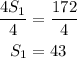
Substitute S₁ in equation 1

`\begin{gathered} S_2=8+S_1 \\ S_2=8+43 \\ S_2=51 \end{gathered}`

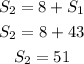
Hence,

The slower car travels at 43 miles per hour(mph), and

The faster car travels as 51 miles per hour(mph)