Question

2. 5.4 grams of carbon dioxide gas is confined to a 20.0 L container at atemperature of 32.5°C. What pressure does the gas exert? (15 kPa)

Answer 1

To calculate this, we will need to assume the gas behaves as an ideal gas.

So, we can use the Ideal Gas Law:

`PV=nRT`

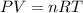
Where P is the pressure, V is the volume, n is the number of moles, is the absolut temperature and R is the gas law constant.

Since we have carbon dioxide, CO₂, we need to calculate its molar mass to convert the mass to number of moles:

`\begin{gathered} M_(CO_2)=(1\cdot M_C+2\cdot M_O) \\ M_(CO_2)=(1\cdot12.0107+2\cdot15.9994)g\/mol \\ M_(CO_2)=44.0095g\/mol \end{gathered}`

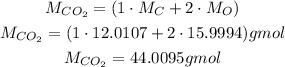
So, the number of moles is:

`\begin{gathered} M_(CO_2)=(m)/(n) \\ n=\frac{m}{M_{CO_(2)}}=(5.4g)/(44.0095g\/mol)=0.1227\ldots mol\approx0.12mol \end{gathered}`

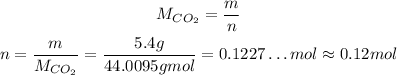
Also, we need to convert the temperature to absolute temperature, so we can convert it to K by adding 273.15 to the degree celcius temperature:

`T=32.5\degree C=(32.5+273.15)K=305.65K`

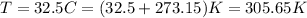
Now, we need to use the constant R that has the unit we want. We have K for temperature, mol for number of moles and L for volume. Is we want the pressure in kPa, we need to use the R constant with units L*kPa/(K*mol), which have the value:

`R\approx8.31446(L\cdot kPa)/(K\cdot mol)`

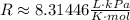
So, solving the equation for P and substituting the values, we have:

`\begin{gathered} PV=nRT \\ P=(nRT)/(V) \\ P=(0.12mol\cdot8.31446L\cdot kPa\cdot K^(-1)mol^(-1)\cdot305.65K)/(20.0L) \\ P=(0.12\cdot8.31446\cdot305.65)/(20.0)kPa \\ P=15.247\ldots kPa\approx15kPa \end{gathered}`

So, the pressure is approximately 15 kPa.