Question

I need help with some problems on my assignment please help

Answer 1

The circumcenter of a triangle is the center of a circumference where the three vertex are included. So basically we must find the circumference that passes through points O, V and W. The equation of a circumference of a radius r and a central point (a,b) is:

`(x-a)^2+(y-b)^2=r^2`

We have three points which give us three pairs of (x,y) values that we can use to build three equations for a, b and r. Using point O=(6,5) we get:

`(6-a)^2+(5-b)^2=r^2`

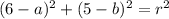
Using V=(0,13) we get:

`(0-a)^2+(13-b)^2=r^2`

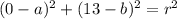
And using W=(-3,0) we get:

`(-3-a)^2+(0-b)^2=r^2`

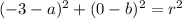
So we have a system of three equations and we must find three variables: a, b and r. All equations have r^2 at their right side. This means that we can take the left sides and equalize them. Let's do this with the second and third equation:

`\begin{gathered} (0-a)^2+(13-b)^2=(-3-a)^2+(0-b)^2 \\ a^2+(13-b)^2=(-3-a)^2+b^2 \end{gathered}`

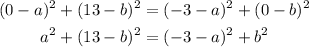
If we develop the squared terms:

`a^2+b^2-26b+169=a^2+6a+9+b^2`

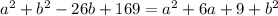
Then we substract a^2 and b^2 from both sides:

`\begin{gathered} a^2+b^2-26b+169-a^2-b^2=a^2+6a+9+b^2-a^2-b^2 \\ -26b+169=6a+9 \end{gathered}`

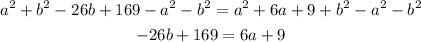
We substract 9 from both sides:

`\begin{gathered} -26b+169-9=6a+9-9 \\ -26b+160=6a \end{gathered}`

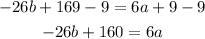
And we divide by 6:

`\begin{gathered} (-26b+160)/(6)=(6a)/(6) \\ a=-(13)/(3)b+(80)/(3) \end{gathered}`

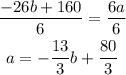
Now we can replace a with this expression in the first equation:

`\begin{gathered} (6-a)^2+(5-b)^2=r^2 \\ (6-(-(13)/(3)b+(80)/(3)))^2+(5-b)^2=r^2 \\ ((13)/(3)b-(62)/(3))^2+(5-b)^2=r^2 \end{gathered}`

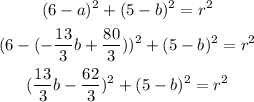
We develop the squares:

`\begin{gathered} ((13)/(3)b-(62)/(3))^2+(5-b)^2=r^2 \\ (169)/(9)b^2-(1612)/(9)b+(3844)/(9)+b^2-10b+25=r^2 \\ (178)/(9)b^2-(1702)/(9)b+(4069)/(9)=r^2 \end{gathered}`

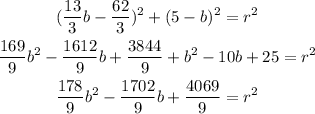
So this expression is equal to r^2. This means that is equal