Diagram 1.
Strategy 1.
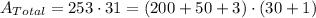
If we add all the areas together we get:
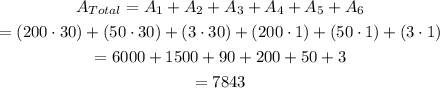
Diagram 2.
Strategy 2.
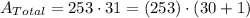
If we add all the areas together we get:
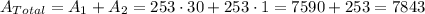
We can see that we got the same answer: Total area = 7843 quare units
The strategies are similar because they are dividing the total area into smaller ones and then add them together.
However, they are different in that diagram 1 has more areas that are smaller compared to diagram 2. Also, the divisions in diagram 1 are designed to make multiplications easier compared to diagram 2.