Question

find the perimeter of the triangle whose vertices are (-10,-3), (2,-3), and (2,2). write the exact answer. do not round.

Answer 1

We have to calculate the perimeter of a triangle of which we know the vertices.

The perimeter is the sum of the length of the three sides, which can be calculated as the distance between the vertices.

The vertices are V1=(-10,-3), V2=(2,-3), and V3=(2,2).

We then calculate the distance between each of the vertices.

We start with V1 and V2:

`\begin{gathered} d_(12)=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ d_(12)=\sqrt[]{(-3-(-3))^2+(2-(-10)^2} \\ d_(12)=\sqrt[]{(-3+3)^2+(2+10)^2} \\ d_(12)=\sqrt[]{0^2+12^2} \\ d_(12)=12 \end{gathered}`

We know calculate the distance between V1 and V3:

`\begin{gathered} d_(13)=\sqrt[]{(y_3-y_1)^2+(x_3-x_1)^2} \\ d_(13)=\sqrt[]{(2-(-3))^2+(2-(-10))^2} \\ d_(13)=\sqrt[]{5^2+12^2} \\ d_(13)=\sqrt[]{25+144} \\ d_(13)=\sqrt[]{169} \\ d_(13)=13 \end{gathered}`

Finally, we calculate the distance between V1 and V3:

`\begin{gathered} d_(23)=\sqrt[]{(y_3-y_2)^2+(x_3-x_2)^2} \\ d_(23)=\sqrt[]{(2-(-3))^2+(2-2)^2} \\ d_(23)=\sqrt[]{5^2+0^2} \\ d_(23)=5 \end{gathered}`

Then, the perimeter can be calcualted as:

`\begin{gathered} P=d_(12)+d_(13)+d_(23) \\ P=12+13+5 \\ P=30 \end{gathered}`

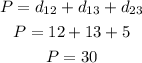
Answer: the perimeter is 30 units.