The rational expression we have is:
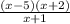
For a rational expression to be equal to 0, the numerator of the expression has to be equal to 0.
The numerator is: (x-5)(x+2)
That has to be equal to 0:

Here, we apply the zero product property, which tells us that if a product is equal to 0, one of the two elements, or the two elements, are equal to 0:
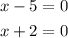
We solve the two equations, and get the two values that will make the rational equation equal to 0:
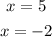
Answer:
E. 5
F. -2