Question

As the table shows, projections indicate that the percent of adults with diabetes could dramatically increase.Answer parts a. through c.c. In what year does this model predict the percent to be 27.96%(round to the closest year)

Answer 1

b. You have to consider year 2000 as the initial year, i.e. as x=0.

To predict the percent of adults with diabetes in 2014, first, you have to calculate the difference between this year and the initial year to determine which value of x you need to use:

`x=2014-2000=\text{ }14`

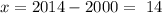
The value of x you have to use is x=14

Replace this value into the linear model calculated in item a to predict the percentage of adults with diabetes (y)

`\begin{gathered} y=0.508x+10.692 \\ y=0.508\cdot14+10.692 \\ y=7.112+10.692 \\ y=17.804 \end{gathered}`

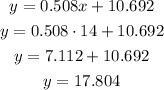
In the year 2014, the predicted percentage of adults with diabetes is 17.8%

c. You have to determine the year in which the model predicts the percent to be 27.96%.

To determine this year, you have to equal the linear model to 27.96% and calculate for x:

`\begin{gathered} y=0.508x+10.692 \\ 27.96=0.508x+10.692 \end{gathered}`

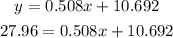
-Subtract 10.692 from both sides of the equal sign

`\begin{gathered} 27.96-10.692=0.508x+10.692-10.692 \\ 17.268=0.508x \end{gathered}`

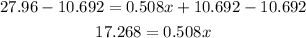
-Divide both sides by 0.508

`\begin{gathered} (17.268)/(0.508)=(0.508x)/(0.508) \\ 33.99=x \\ x\approx34 \end{gathered}`

Next, add x=34 to the initial year:

`2000+34=2034`

The model predicts the percentage to be 27.96% for the year 2034